Format Data
Many elements have a Format attribute that lets developers specify how its data will be formatted. The most common of these, for example, is the Label element. Applying a formatting to a Label caption is especially useful for dates, times, and certain types of numbers. This topic explains the available options.
- About Formatting
- Standard Formats
- Custom Date and Time Formats
- Custom Numeric Formats
- The Formatted Column Element
About Formatting
The following elements have a Format attribute, which can be set to format the appearance of their data:
- Analysis Grid Column
- Crosstab Table Value Column
- Format Font
- Formatted Column
- Gauge Label
- Heat Map Column
- Input Date, Input Text, Input Text Area
- Label
- Mdx Calculated Measure
- Pdf Form Field
- Schedule
- Word Form Field
Two chart-related elements, Format Data and Format Label, have Format attributes and were deprecated in v10.2.424. They were replaced by the addition of a Format attribute to the Label Scale and Data Scale elements.
Logi Studio is not always context-sensitive when it comes to the options available for Format attributes, so it may be possible to select formatting options that are not appropriate for the data.
See Format Classic Chart Label for more information about chart title and label formatting techniques for special effects such as sub- and super-scripting, mixing fonts and colors, and stacking text.
Many of the formatting types available are drawn from the Microsoft Visual Basic predefined format types and are dependent on the Regional settings in the web server's operating system.
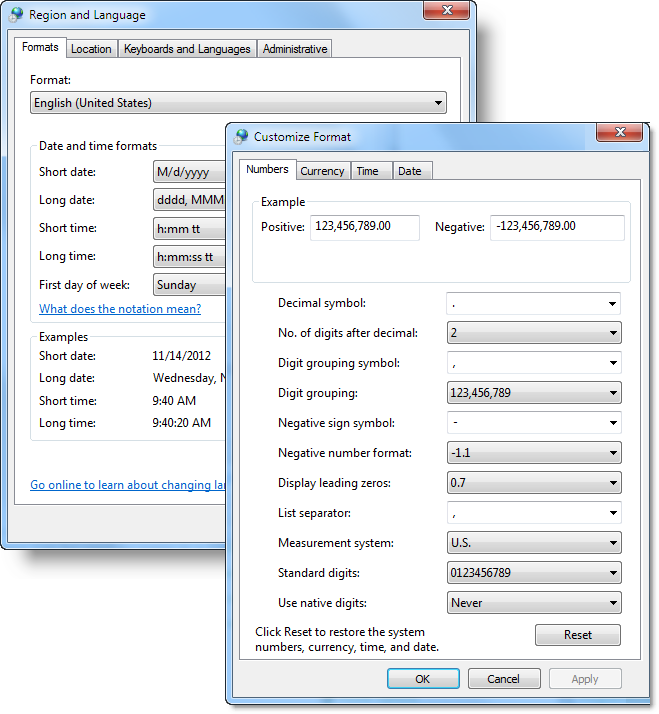
For example, as shown above, Regional and Language options are available on Windows-based web servers through the Control Panel. The "Currency", "Short date" and "Long date" formats defined here can be used by name in a Format attribute.
Standard Formats
The following standard formats are available, from a pull-down list, in Studio for elements' Format attribute value:
| Type | Description |
|---|---|
< | Converts all characters to lower-case. |
> | Converts all characters to upper-case. |
Expanded Spaces | Preserves space characters that are normally collapsed by the web browser. This formatting will not be applied if used with content that includes more than one @Data token. |
Preserve Line Feeds | Preserves line breaks (CTRL-ENTER). This formatting will not be applied if used with content that includes more than one @Data token. |
HTML | Preserves HTML tags, embedding them rather than encoding them. Text appearance and alignment is affected by the tags; they are not seen in the text. |
General Date | Display a date and/or time. For real numbers, display a date and time, for example, 4/3/93 05:34 PM. If there is no fractional part, display only a date, for example, 4/3/93. If there is no integer part, display time only, for example, 05:34 PM. Date display is determined by the web server's settings. |
| Long Date | Display a date according to the web server's Long Date format. |
Medium Date | Display a date using the Medium Date format appropriate for the language version of the host application on the web server. |
Short Date | Display a date using web servers's Short Date format. |
Long Time | Display time using the web server's Long Time format; includes hours, minutes, seconds. |
Medium Time | Display time in 12-hour format using hours and minutes and the AM/PM designator. |
Short Time | Display time using the 24-hour format, for example, 17:45. |
| yyyy/MM/dd | A custom date/time format defined by the developer using the components described in the next section. |
| hh:mm | Display time as hours and minutes, with leading zeroes. Example: 01:08 |
| yyyy/MM/dd hh:mm:ss | Display date and time, with leading zeroes. Example: 2007/01/01 01:08:02 |
| General Number | Display number with no thousands separator. |
| Currency | Display number with thousands separator, if appropriate; display two digits to the right of the decimal separator. Output is based your system locale settings. |
| Fixed | Display at least one digit to the left and two digits to the right of the decimal separator. |
| Standard | Display number with thousands separator, at least one digit to the left and two digits to the right of the decimal separator. |
| Percent | Display number multiplied by 100 with a percent sign (%) appended to the right; always display two digits to the right of the decimal separator. |
| Scientific | Use standard scientific notation. |
| mp | Formats numbers by applying the appropriate "metric prefixes" (giga-, mega-, kilo-, etc.). Example: "1,234,567" formatted with "$#.00mp" produces "$1.23M". More information about metric prefixes can be found here. Customization of the mp format can be accomplished using the Globalization element's Metric Prefix String attribute, see Internationalization and Localization. (v10.2.424+) |
| ###,###,##0.00 | Display number with thousands separator for every three digits to left, at least one digit to the left and two digits to the right of the decimal separator. |
| Yes/No | Display No if number is 0; otherwise, display Yes. |
| True/False | Display False if number is 0; otherwise, display True. |
| On/Off | Display Off if number is 0; otherwise, display On. |
The HTML format, when used with a Label caption, allows you to embed HTML code in the report. This be used to accomplish things as simple as making part of a line bold-faced using <B> tags, or as complicated as including scripts within <SCRIPT> tags for various purposes. When using the HTML format, ensure that you do not include a <BODY> tag that might confuse the Logi Server Engine when it generates its HTML output.
Hint: Use these standard date/time and numeric formats to improve performance with large reports.
Note that the standard numeric formats, such as Currency, may cause rounding, and this may affect aggregations and summaries of the data.
Custom Date and Time Formats
In addition to the standard formats listed above, developers can enter custom date and time formats by typing them in directly.
For example, one of the standard date formats is "yyyy/MM/dd". Developers can directly enter other combinations of valid formatting characters, such as "MM/dd/yyyy" to obtain the desired format. Note that format values are case-sensitive and are not entered with quotation marks. Here are the valid date and time formatting characters:
| Chars | Description |
|---|---|
| : | Time separator. In some locales, other characters may be used to represent the time separator. The time separator separates hours, minutes, and seconds when time values are formatted. The actual character used as the time separator in formatted output is determined by the client OS locale setting. |
| / | Date separator. In some locales, other characters may be used to represent the date separator. The date separator separates the day, month, and year when date values are formatted. The actual character used as the date separator in formatted output is determined by the client OS locale setting. |
| % | Used to indicate that the following character should be read as a single-letter format without regard to any trailing letters. Also used to indicate that a single-letter format is read as a user-defined format. See below for further details. |
| d | Day as a number, without a leading zero: 1. Use %d if this is the only character in your user-defined numeric format. |
| dd | Day of month number, with leading zero: 04 |
| ddd | Three-letter abbreviation of day name: Wed |
| dddd | Full day name: Thursday |
| M | Full month name and day combination: July 22 |
| MM | Month number: 07 |
| MMM | Three-letter month name abbreviation: Jul |
| MMMM | Full month name: September |
| gg | The period/era: A.D. Note that this is not available in Format Label and Format Data elements. |
Quarter number: 1, 2, 3, or 4. Note that this is not available in Format Label and Format Data elements. | |
| y | Year number (0-9), without leading zeros. Use %y if this is the only character in your user-defined numeric format. |
| yy | Two-digit year, with a leading zero, but without century: 09 |
| yyyy | Four-digit year: 2009 |
| h | Hour as a number, without a leading zero, using the 12-hour clock: 1:15:15 PM. Use %h if this is the only character in your user-defined numeric format. |
| hh | Hour as a number, with a leading zero, using the 12-hour clock: 04 |
| H | Hour as a number, without a leading zero, using the 24-hour clock: 13:15:15 PM. Use %H if this is the only character in your user-defined numeric format. |
| HH | Hour as a number, with a leading zero, using the 24-hour clock: 01 |
| m | Minute as a number, without leading zeros: 12:1:15. Use %m if this is the only character in your user-defined numeric format. |
| mm | Minute as a number, with leading zeros: 12:01:15 |
| s | Second as a number, without leading zeros: 12:1:5. Use %m if this is the only character in your user-defined numeric format. |
| ss | Second as a number, with a leading zero: 12:1:05 |
| f | Fractions of a second. For example, ff will display hundredths of seconds, whereas ffff will display ten-thousandths of seconds. You may use up to seven f symbols in your user-defined format. Use %f if this is the only character in your user-defined numeric format. |
| T | Uses the 12-hour clock and displays an uppercase |
| t | Hour and minute with AM/PM designator: 10:32 AM |
| tt | AM or PM designator alone: PM |
| z | Timezone offset as a number, without a leading zero: -8. Use %z if this is the only character in your user-defined numeric format. |
| zz | Timezone offset as a number, with a leading zero: -08 |
| zzz | Full timezone offset as a number, with a leading zero: -08:00 |
Visit the MSDN Library User Defined Date/Time Formats page for more information.
Custom Numeric Formats
In addition to the standard formats listed above, developers can enter custom numeric formats by typing them in directly.
For example, one of the standard date formats is "###,###,##0.00". Developers can directly enter other combinations of valid formatting characters, such as "$#,##0" to obtain the desired format. Here are the valid numeric formatting characters:
| Chars | Description |
|---|---|
| None | Displays the number with no formatting. |
| 0 | Digit placeholder. Displays a digit or a zero. If the expression has a digit in the position where the zero appears in the format string, display it; otherwise, displays a zero in that position. If the number has fewer digits than there are zeros (on either side of the decimal) in the format expression, displays leading or trailing zeros. If the number has more digits to the right of the decimal separator than there are zeros to the right of the decimal separator in the format expression, rounds the number to as many decimal places as there are zeros. If the number has more digits to the left of the decimal separator than there are zeros to the left of the decimal separator in the format expression, displays the extra digits without modification. |
| # | Digit placeholder. Displays a digit or nothing. If the expression has a digit in the position where the # character appears in the format string, displays it; otherwise, displays nothing in that position. This symbol works like the 0 digit placeholder, except that leading and trailing zeros aren't displayed if the number has fewer digits than there are # characters on either side of the decimal separator in the format expression. |
| . | Decimal placeholder. The decimal placeholder determines how many digits are displayed to the left and right of the decimal separator. If the format expression contains only # characters to the left of this symbol; numbers smaller than 1 begin with a decimal separator. To display a leading zero displayed with fractional numbers, use zero as the first digit placeholder to the left of the decimal separator. In some locales, a comma is used as the decimal separator. The actual character used as a decimal placeholder in the formatted output depends on the number format recognized by your system. Thus, you should use the period as the decimal placeholder in your formats even if you are in a locale that uses a comma as a decimal placeholder. The formatted string will appear in the format correct for the locale. |
| % | Percent placeholder. Multiplies the expression by 100. The percent character (%) is inserted in the position where it appears in the format string. |
| , | Thousand separator. The thousand separator separates thousands from hundreds within a number that has four or more places to the left of the decimal separator. Standard use of the thousand separator is specified if the format contains a thousand separator surrounded by digit placeholders (0 or #). A thousand separator immediately to the left of the decimal separator (whether or not a decimal is specified) or as the rightmost character in the string means "scale the number by dividing it by 1,000, rounding as needed." For example, you can use the format string Multiple separators in any position other than immediately to the left of the decimal separator or the rightmost position in the string are treated simply as specifying the use of a thousand separator. In some locales, a period is used as a thousand separator. The actual character used as the thousand separator in the formatted output depends on the Number Format recognized by your system. Thus, you should use the comma as the thousand separator in your formats even if you are in a locale that uses a period as a thousand separator. The formatted string will appear in the format correct for the locale. |
| E- E+ e- e+ | Scientific format. If the format expression contains at least one digit
placeholder (0 or #) to the left of E-, E+,
e-, or e+, the number is displayed in scientific format and |
| - + $ ( ) | Literal characters. These characters are displayed exactly as typed in the format string. To display a character other than one of those listed, precede it with a backslash (\) or enclose it in double quotation marks (" "). |
| \ | Displays the next character in the format string. To display a character that has special meaning as a literal character, precede it with a backslash (\). The backslash itself isn't displayed. Using a backslash is the same as enclosing the next character in double quotation marks. To display a backslash, use two backslashes (\\). Examples of characters that can't be displayed as literal characters are the date-formatting and time-formatting characters (a, c, d, h, m, n, p, q, s, t, w, y, /, and :), the numeric-formatting characters (#, 0, %, E, e, comma, and period), and the string-formatting characters (@, &, <, >, and !). |
Visit the MSDN Library User Defined Numeric Formats page for more information.
Positive and Negative Number Formatting
To construct a custom format for currency or numbers that treats positive and negative numbers differently, use a semi-colon and a space in the Format attribute to delineate two formats:
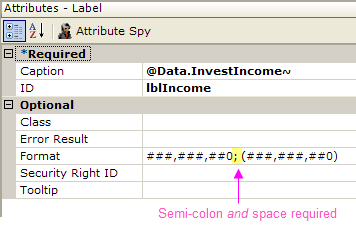
For example, the Format value shown above will show positive numbers with a comma as a thousands separator. It will show negative numbers in the same way but also enclose them in parenthesis. Note the semi-colon and space which separate the positive and negative formats.
You can also use the Conditional Class element, beneath any Label element that displays numeric data, to display negative numbers in a different color than positive numbers.
The Formatted Column Element
A special element, the Formatted Column element, allows developer to format data right in a datalayer. The element formats data from another column and places it in a new column in the datalayer. All of the formatting options previously discussed here are available in this element and using the Formatted Column can produce report performance improvements.
For more information, see The Formatted Column.