Forecasting Methodologies
This topic provides some insight into the methods used inside Logi Forecasting elements.
- About Forecasting
- Regression
- Prorating
- Time Series Decomposition
About Forecasting
Forecasting is the process of making statements about events whose actual outcomes (typically) have not yet been observed. A commonplace example might be estimation for some variable of interest at some specified future date. Prediction is a similar, but more general term.
The source data used in forecasting may be:
- Causal: A dataset ordered by an independent variable, where an independent variable and a dependent variable are numbers. The independent variable may or may not have strong interval, such as 1, 5, 14, 23, 72. For example, the number of unique web site visitors and a count of the clicks on each ad.
- Time Series: A natural temporal ordering with a strong interval, where an independent variable (X-axis) is of DateTime type and a dependent variable (Y-axis) is a number. For example, Product Sales by Month.
Which Method is Right?
There is no single "right" forecasting method and the number of usable methods is huge. For example, Wikipedia displays the following list of methods for Time Series forecasting alone:
- Moving Average
- Weighted Moving Average
- Exponential Smoothing
- Autoregressive Moving Average
- Autoregressive Integrated Moving Average (Box-Jenkins)
- Extrapolation
- Linear Prediction
- Trend Estimation
- Growth Curve
- Regression Analysis
Some of these methods are simple to understand, but others are not. For example, the Moving Average method, by itself, is not that useful for forecasting, because its forecasts will have tendency to show just the "average" line. However, the Autoregressive Integrated Moving Average method is difficult for end-users to understand, as it requires the definition a number of constants, including Autoregression Lag, Integration Parameter, and Moving Average Parameter, and there is no "right" way to determine these parameters automatically.
Logi Forecasting elements use three methods of implementing forecasting calculations, which utilize a mix of the methods listed earlier:
- Regression (for Casual data)
- Prorating (for Time Series data)
- Time Series Decomposition (for Time Series data)
Our implementation of these methods is discussed in the following sections.
Regression
Linear prediction is a mathematical operation in which the future values of a dependent variable are estimated as a function of previous samples. The Forecast.Regression element implements:
- Simplelinear regression, where values are based on a trend line
- Autoregression, which predicts an output based on previous outputs, using the "Burg" method
- Non-linear regression, which displays the relationship between dependent and independent variables using a curvilinear function and may provide more accuracy. Available curvilinear functions include:
- Exponential
- Logarithmic
- Polynomial2
- Polynomial3
- Polynomial4
- Polynomial5
- Power
Input Data Requirements
Data should conform to the following requirements:
- Dependent data column data should be Numeric data type
- Dependent data column data should not contain NULL values
- Independent data column may have any data type (if data type is not Numeric, independent data column will be replaced with an integer enumeration (1,2,3,...RowCount).
- Dataset should be in ascending order by independent data column value
- Forecast Length attribute should be less than original row count (if user defines Forecast Length as more than row count, Forecast Length value will automatically be truncated to 20% of RowCount)
- Some of the regression methods require a minimum number of rows (for example, Autoregression requires at least one more row than the value of the AutoRegressive Order attribute, and Polynomial3 requires at least four rows)
Results
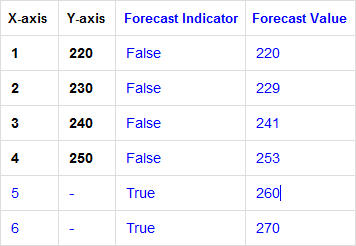
As a result of the forecast operation, two new columns will be added to the datalayer. The names of these two columns will be drawn from the element's attributes:
- Forecast Indicator Column ID: this column will contain a boolean flag, set to True if the row contains a forecast value
- Forecast Value Column ID: this column will contain the forecast value for each row of the original dataset
The following table shows the effect on the datalayer of a forecast operation:
Prorating
The Forecast.Current Time Period element produces its forecast by analyzing a value from the last row in the dataset and "prorating" it into the future, through completion of a specific time period.
Input Data Requirements
Data should conform to the following requirements:
- Dependent data column data should have Numeric data type
- Dependent data column data should not contain NULL values
- Independent data column should have DateTime or Date data type
- Dataset should be in ascending order by independent data column value
Method Implementation
An example, assuming Data Column value = "300", Time Period = "Month", and Current DateTime = "01/10/2014":
- Determine start of date period (current month start): 01/01/2014
- Determine the end of date period (current month end): 01/31/201
- Calculate number of seconds between date period start and current date: 01/10/2014 - 01/01/2014 = 86,400 (seconds per day) * 10 days = 864,000 seconds
- Calculate data value for one second: 300 / 86,4000 = ~0.00034
- Calculate number of seconds between current date and date period end: 01/31/2014 - 01/10/2014 = 1,814,400 seconds
- Determine predicted value by multiplying number of seconds between current date and date period end, and data value for one second: 0.00034 * 1,814,400 = ~616
- Save predicted value to column identified by Forecast Difference Column ID attribute.
- Save sum of predicted value and actual data value (300 + ~616) to column identified by Forecast Value Column ID attribute.
Results
As a result of the forecast operation, three new columns will be added to the datalayer. The names of these columns will be drawn from the element's attributes:
- Forecast Difference Column ID: this column will contain the value of the difference between the starting data value and each prorated value
- Forecast Indicator Column ID: this column will contain a boolean flag, set to True if the row contains a forecast value
- Forecast Value Column ID: this column will contain the forecast value for each row of the original dataset (if this value is left blank, the forecast values will be added to the value of the dependent Data Column)
Time Series Decomposition
The decomposition of time series data is a statistical method that deconstructs it into notional components. Several decomposition methods exist and the Logi Forecast.Time Period Decomposition element uses "Decomposition Based on Rates of Change".
This is an important technique for all types of time series analysis, especially for seasonal adjustment. It seeks to construct, from an observed time series, a number of component series (that could be used to reconstruct the original by additions or multiplications) where each of these has a certain characteristic or type of behaviour. For example, Monthly or Quarterly economic time series are usually decomposed into:
- a Trend Component T that reflects the long term progression of the series
- a Cyclical Component C that describes repeated but non-periodic fluctuations, possibly caused by the economic cycle
- a Seasonal Component S that reflects seasonality (seasonal variation)
- an Irregular Component I that describes random, irregular influences (or "noise"). Compared to the other components it represents the residuals of the time series.
The equation used in the method is: Y = T * S * C * I
Input Data Requirements
Data should conform to the following requirements:
- Dependent data column data should have Numeric data type
- Dependent data column data should not contain NULL values
- Independent data column should have DateTime or Date data type
- Dataset should be in ascending order by independent data column value
- Forecast Length attribute should be less than original row count (if user defines Forecast Length as more than row count, Forecast Length value will automatically be truncated to 20% of RowCount)
- Source rows count should be not less than season count
Data Validation
It's necessary to check the dataset for inconsistencies before running the forecasting algorithm. "Empty spaces" inside time series are not allowed, a validation process checks the dataset in advance. If an iteration includes more than three "empty spaces", such as "Jan, Feb, July, Aug...", validation returns an error. Otherwise, validations fills missing time periods with the average of the values for the previous and next period. For example, the following dataset,
which is missing data for February:
| Iteration | Source Data |
|---|---|
| January | 10 |
| March | 30 |
| April | 40 |
becomes
| Iteration | Source Data | Validated Data |
|---|---|---|
| January | 10 | 10 |
| February | 20 | |
| March | 30 | 30 |
| April | 40 | 40 |
Time Series Iteration
Time Series Decomposition requires defined date iteration, which is necessary for the determination of the seasonal component. These date iterations are used:
| Iteration | Season Count | Season Determination |
|---|---|---|
| Hour | 24 | Hour |
| Day | 7 | Day of Week |
| Week | 5 | Week of Month |
| Month | 12 | Month |
| Quarter | 4 | Quarter |
| Year | 1 | No season |
Method Implementation
- "Deseasonalizing" the data: Remove short-term fluctuations from the data, so that the longer-term trend and cycle components can be more clearly identified. These short-term fluctuations include both seasonal patterns and irregular variations. They can be removed by calculating an appropriate Moving Average (MA) for the series, which should contain the same number of periods as there are in the seasonality that we want to identify. If the season count is an even number, the moving averages are not really centered in the middle of the seasons. We calculate a Centered Moving Average (CMA) and it represents the deseasonalized data.
- Determine Seasonical Factor (SF), which is the ratio of the actual value to the deseasonalized value.
- Create Season Index (SI) for each season, which is the normalized mean of the seasonal factors for the selected season.
- Estimate Long Term Trend from the deseasonalized data using linear regression.
- The cyclical component of a time series is the extended wavelike movement about the long-term trend. It is measured by the Cycle Factor (CF), which is the ratio of the Centered Moving Average to the Long Term Trend.
- Determine forecast for Cyclical component by using AutoRegression with Order equal to the Count of seasons (use 4 if no season).
- Calculate forecast for time series.
Results
As a result of the forecast operation, two new columns will be added to the datalayer. The names of these two columns will be drawn from the element's attributes:
- Forecast Indicator Column ID: this column will contain a boolean flag, set to True if the row contains a forecast value
- Forecast Value Column ID: this column will contain the forecast value for each row of the original dataset